平稳随机过程的自相关函数(平稳随机过程的功率谱密度)
平稳随机过程的自相关函数,并给出了一种基于随机过程的模糊控制器设计 *** 。仿真结果表明,该 *** 能有效地减小系统响应时间,提高系统稳定性。文中还介绍了了该 *** 的应用实例。最后,给出了一个典型的实例。通过仿真分析,证明了该 *** 的有效性。本文的研究成果对于提高模糊控制器的鲁棒性改善系统的稳定性具有重要意义。同时,也为进一步开发新型智能控制器提供了理论依据。
1.ARIMA模型
差分平稳序列在经过差分后变成平稳时间序列,之后的分析可以用ARMA模型进行,差分过程加上ARMA模型对差分平稳序列进行的分析称为ARIMA模型。
【1】先观测序列的时序图,可知序列具有线性长期趋势,需要进行1阶差分。
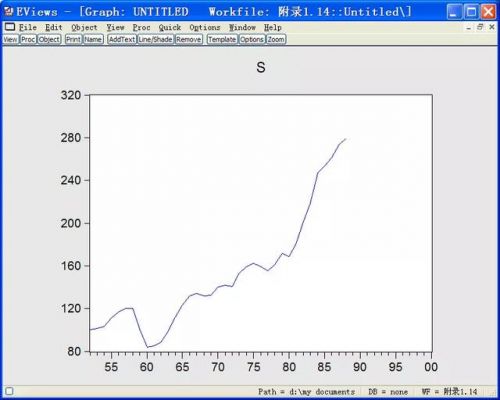
图1:1952-1988年中国农业实际国民收入指数时序图
图2:1阶差分后序列的时序图
图3:1阶差分后序列的相关分析
由图可知,序列1阶自相关显著,序列平稳;Q统计量P值小于0.05,非白噪声;同时,偏自相关拖尾、自相关一步截尾,建立ARIMA(0,1,1)模型。建立ARIMA(0,1,1)模型,是因为偏自相关拖尾,所以第一个数值为0,然后因为序列进行了一阶差分,所以中间数值为1,又自相关图一阶截尾,所以最后一个数值1。
【3】建模分析
图4:ARIMA(0,1,1)模型
图5:模型残差的相关性分析
从图4和图5分析可知,残差为白噪声,模型信息提取充分;模型参数显著,模型精简,因此建立的ARIMA(0,1,1)模型合格,模型具体情况如下式:
(1-B)S=5.0156+(1-0.7082B)
【4】预测分析
图6:预测1989-2000年农业实际国民收入指数
图7:1989-2000年农业实际国民收入指数预测图
2.季节模型
2.1简单季节模型
对1962.1——1975.12平均每头奶牛月产奶量序列进行分析,根据上期的分析可知,经过1阶12步差分后,op变成平稳时间序列。
图1:序列D(OP,1,12)的相关分析图
经过相关分析看出自相关图具有短期相关性,是平稳时间序列;Q统计量的P值有小于0.05的情况,因此序列为平稳非白噪声序列。又通过观测自相关和偏自相关图,识别方程为一阶自回归方程。
图2:序列D(OP,1,12)的AR(1)模型
图3:模型残差的相关分析
分析可知残差为白噪声,因而模型提取信息充分;观测图2可知模型参数显著,因而AR(1)模型可以提取平稳序列D(OP,1,12)的信息。
模型的具体信息为
2.2乘积季节模型
当序列中长期趋势、季节效应、随机波动可以很容易分开,我们用简单季节模型进行分析;但更为常见的是序列的三个部分不能简单分开,而是相互关联,这时要用乘积季节模型。
对1948-1981年美国女性(大于20岁)月度失业率序列进行分析,首先观测序列的时序图。
图1:1948-1981年美国女性(大于20岁)月度失业率序列时序图
由时序图可知,序列既有长期趋势又有周期性,因此进行1阶12步差分。
图2:进行1阶12步差分
图3:D(S,1,12)的时序图
从时序图可以看出D(S,1,12)均值稳定,也没有明显的周期性,方差有界;通过相关分析,具体分析序列的平稳性如图4。图4中可以看出自相关两阶显著,但是12阶也是显著的,因此在趋势平稳中又包含了周期性因素。
图4:D(S,1,12)的相关分析
用ARMA模型拟合序列D(S,1,12)尝试如下:
图5:AR(1,12)模型拟合序列D(S,1,12)
图6:AR(1,12)模型拟合序列D(S,1,12)的残差相关图
可以看出模型残差非白噪声,模型提取信息不充分。
图7:MA(1,12)模型拟合序列D(S,1,12)
图8:MA(1,12)模型拟合序列D(S,1,12)残差相关图
可以看出模型残差也非白噪声,模型提取信息不充分。
这种情况下我们尝试乘积季节模型。
图9:ARMA(1,1)×(1,0,1)拟合序列D(S,1,12)
图10:ARMA(1,1)×(1,0,1)模型的参数
可以看出SAR(12)的参数并不显著,因此删除该项。
图11:ARMA(1,1)×(0,0,1)拟合序列D(S,1,12)
图12:ARMA(1,1)×(0,0,1)模型的参数
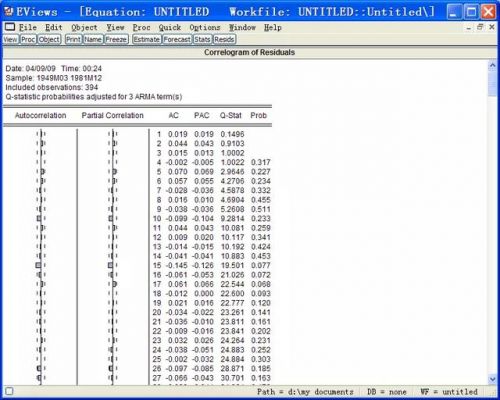
图13:乘积模型的残差相关图
可以看出乘积模型的残差为白噪声序列,该模型提取序列的信息充分;参数都显著,因此模型精简;模型的具体形式为:
