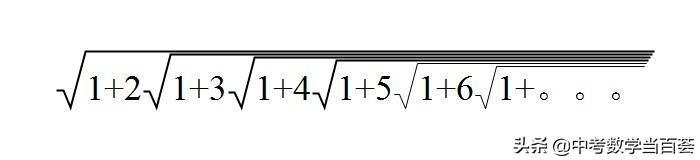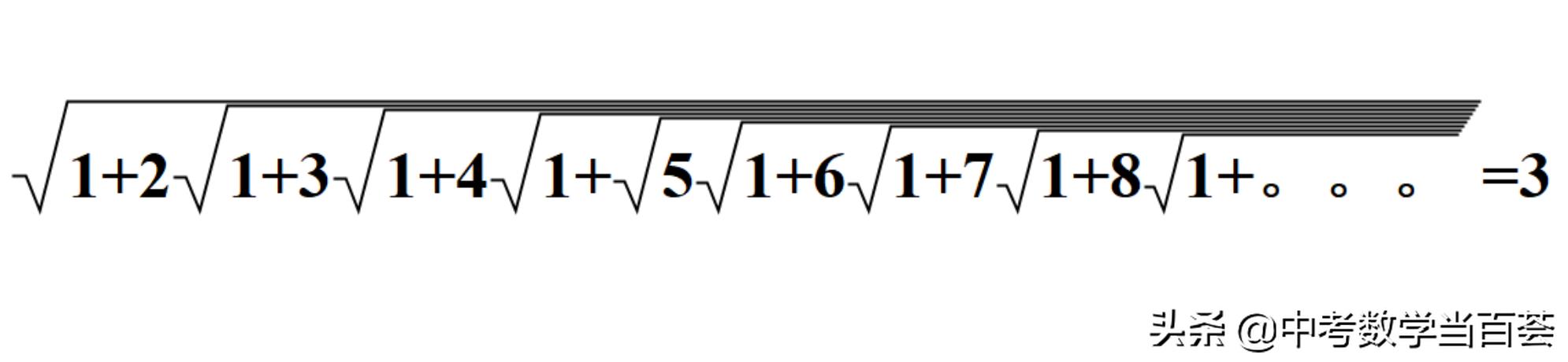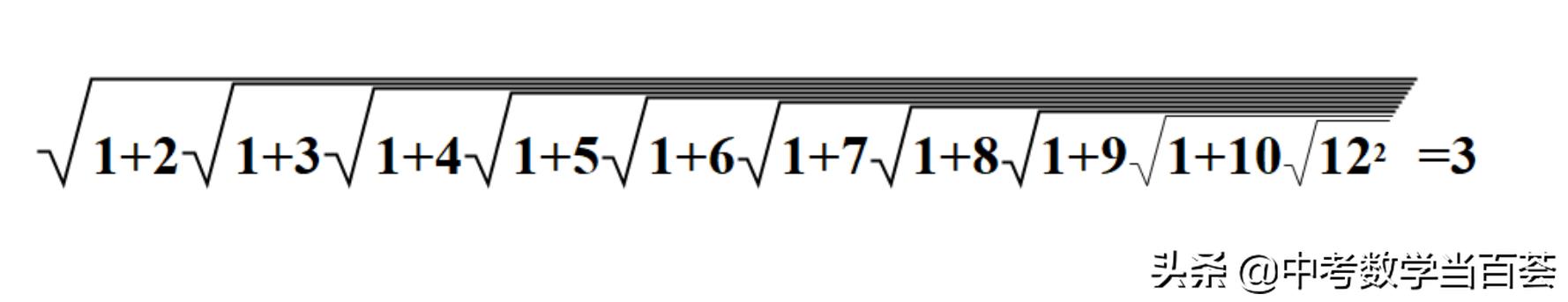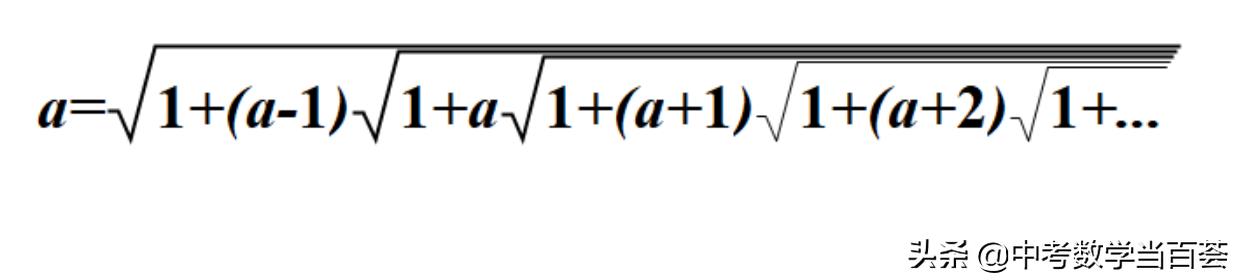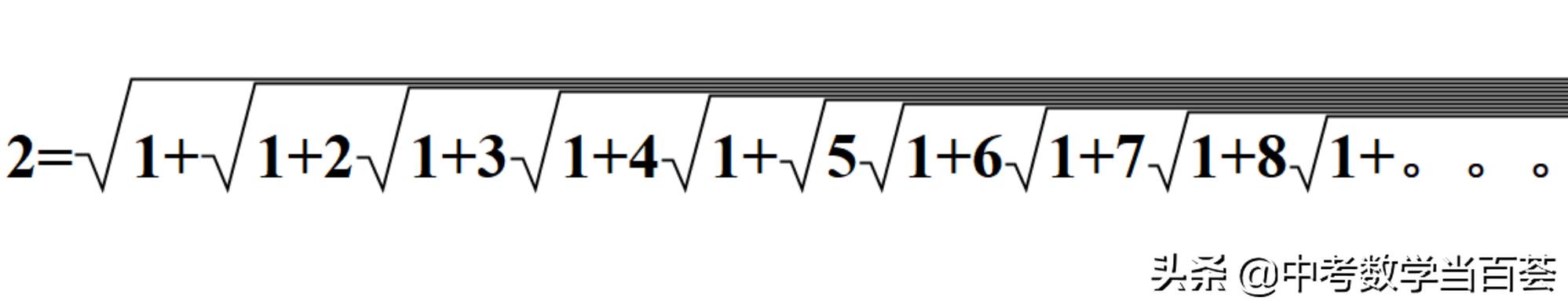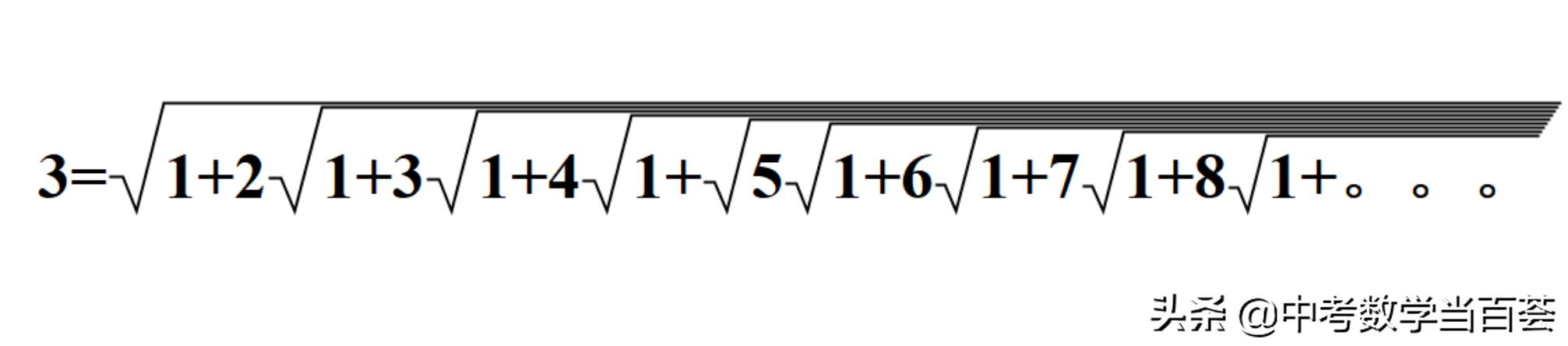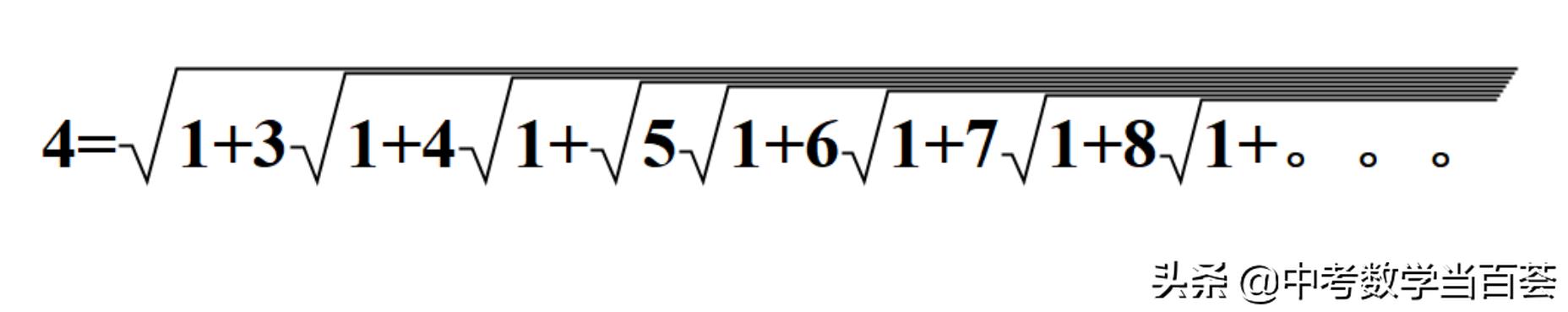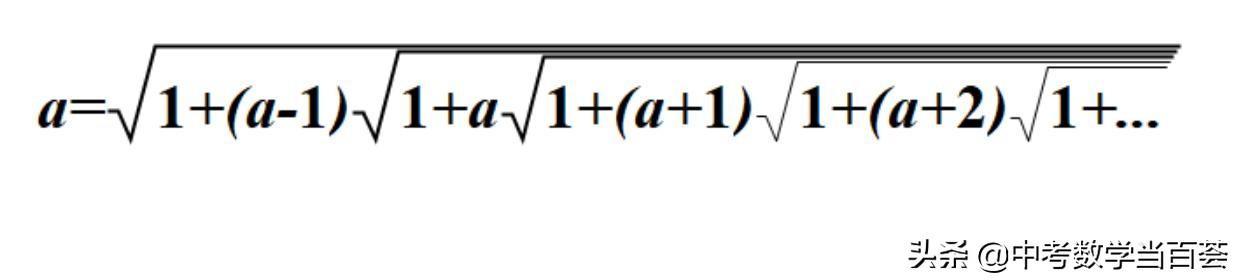​拉马努金恒等式，一个初中生能看懂并能证明的神奇公式

陆佳号

拉马努金恒等式，一个初中生能看懂并能证明的神奇公式



-01-拉马努金恒等式

2016年4月8日在英国上映了一部名叫《知无涯者》的电影。电影讲述了印度数学家斯里尼瓦瑟·拉马努金（1887.12.22~1920.4.26），

短暂而传奇的一生。拉马努金出生贫寒，没有受过专门的数学训练，但天资聪颖，完全靠自学。直到1913年，得到英国数学家哈代的赏识，他的数学才华大放异彩。但他不同于传统意义上数学家，他的成果往往是凭直觉得到，只有结论，而没有证明。他短暂的一生发现了3900条数学公式和命题，许多结果完全是新颖的、原始的和非传统的，但被后续证明他的结论都是正确的。

本文要介绍的这个恒等式，就是拉马努金流传最广的成果之一。先看这个恒等式的一边：


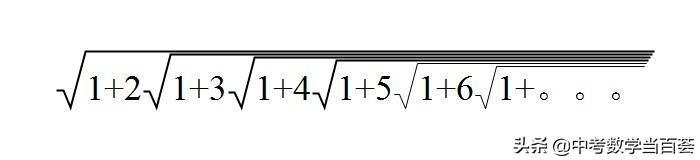
我相信大多数人能按照这个式子的规律接着写下去，但会发现这是无穷尽的，并且很好奇这个式子的结果到底是多少？

拉马努金说，这个式子的结果等于3。

他对形如上式的无穷二次根式，进行深入研究得到这个结果，并且将此发表在《印度数学会刊》上征集证明，数月内无人能应。


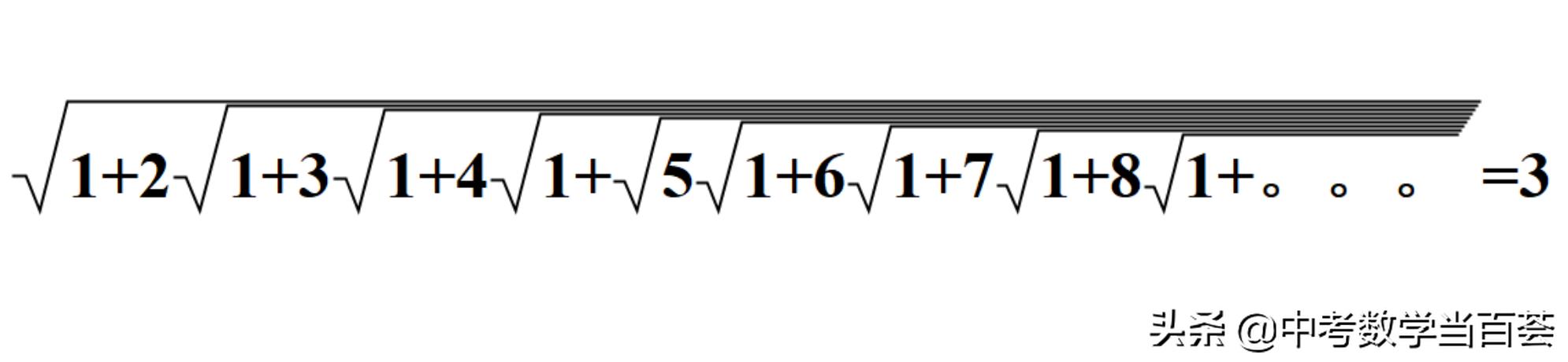
-02-拉马努金恒等式的数学逻辑

下面我们以今天中学生的认知来看其中的数学逻辑：

3=√9。。。。。一层根号

=√1+8

=√1+2x4

=√1+2√16。。。。二层根号

=√1+2√1+15

=√1+2√1+3x5

=√1+2√1+3√25。。三层根号

=√1+2√1+3√1+24

=√1+2√1+3√1+4x6

=√1+2√1+3√1+4√36。四层根号

。。。。。。

由此不难发现：将3拆分后，含n层根号时，3=

√1+2√1+。。。n√（n+2）²

。。。n层根号

验证一下，n=10时（由外向内数，含10层根号），壮观景象：


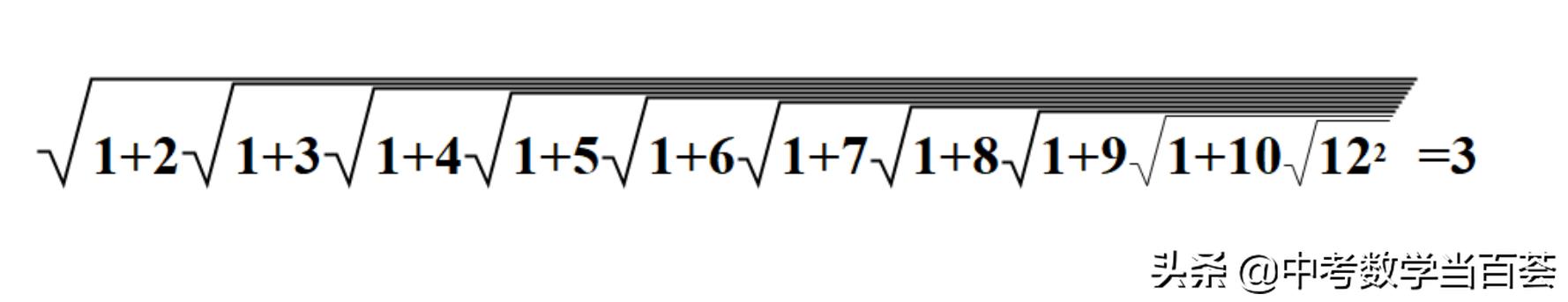
第10层根号里的数：

12²=144；

第9层根号里的数：

11²=121；

第8层根号里的数：

10²=100；

。。。

第3层根号里的数：

5²=25；

第2层根号里的数：

4²=144；

第1层根号里的数：

3²=9；

√9=3

理所当然是个恒等式。

-03-拉马努金恒等式的数学证明

问题来了，正整数3可以象这样用二次根式进行无穷拆分，那么其他正整数呢？他是怎么想到了呢？

平方差公式是初中代数中的最基本的公式之一：

a²-1=(a-1)(a+1)；

变形得

a²=1+(a-1)(a+1)；

即

a=√1+(a-1)(a+1)。

建立一个关于a的函数：

F（a）=a=√1+(a-1)(a+1)，则

F（a+1）=a+1

=√1+(a+1-1)(a+1+1)

=√1+a(a+2)

=√1+aF(a+2)，

F（a+2）=a+2

=√1+(a+2-1)(a+2+1)

=√1+(a+1)(a+3)

=√1+(a+1)F(a+3),

F（a+3）=a+3

=√1+(a+3-1)(a+3+1)

=√1+(a+2)(a+4)

=√1+(a+2)F(a+4)，

...

F（a+n）=a+n

=√1+(a+n-1)(a+n+1)

=√1+(a+n-1)F(a+n+1)，

...

通过层层嵌套，得到

F(a)=√1+(a-1)F(a+1)

=√1+(a-1)√1+aF(a+2)

=√1+(a-1)√1+a√1+(a+1)F(a+3)

...

=√1+(a-1)√1+a√1+(a+1)√1+(a+2)√1+。。。

即


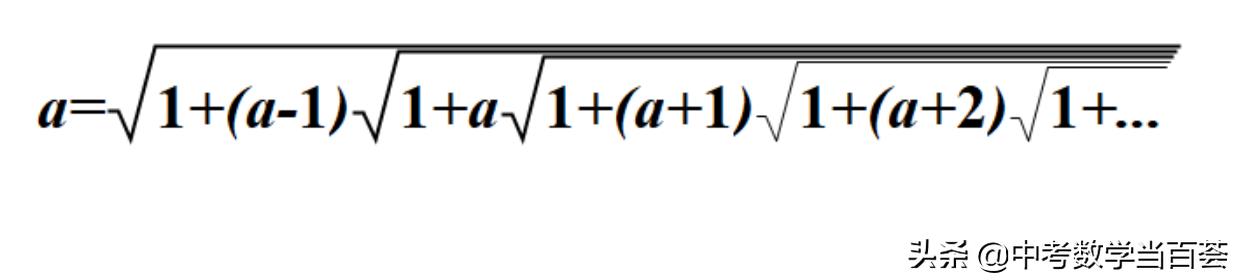
其中，a为正整数。

当a=2时，得到


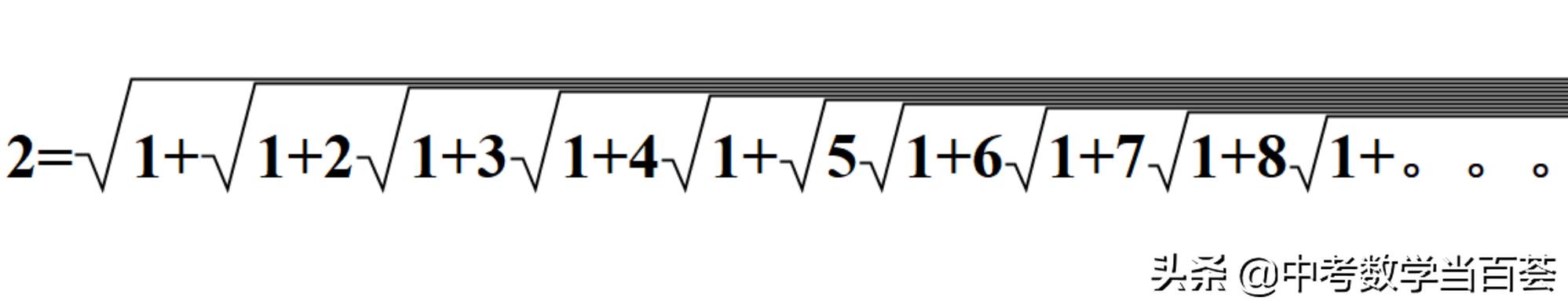
当a=3时，得到


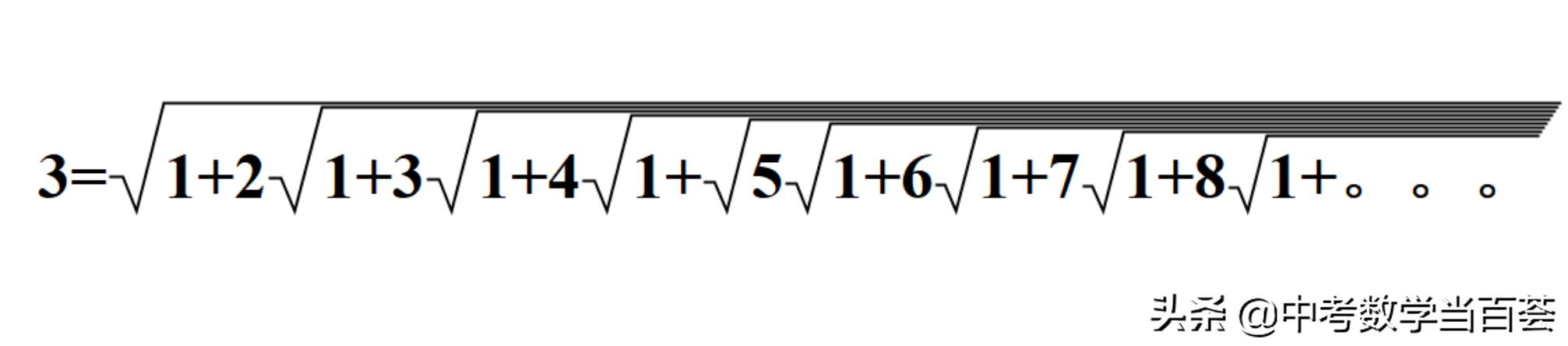
当a=4时，得到


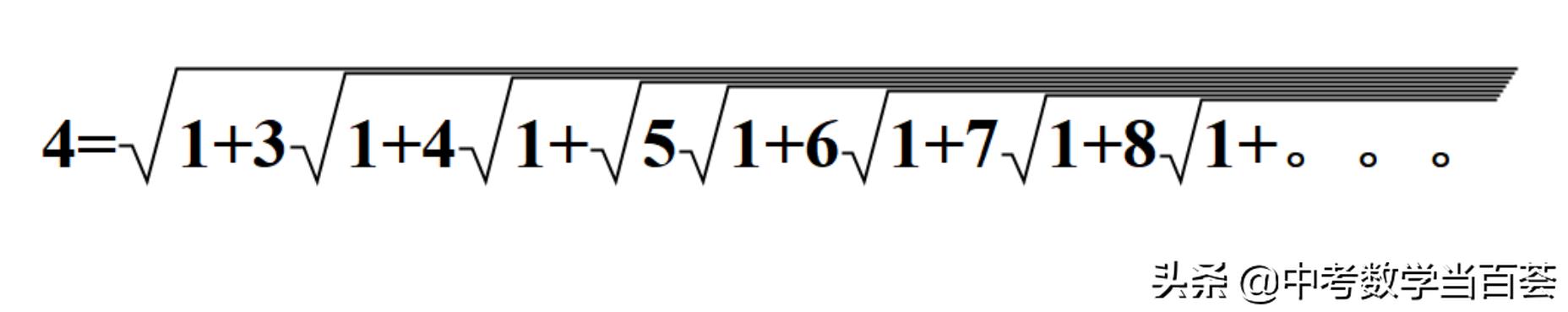
由此，可以把任意一个正整数，用二次根式有规律地无穷展开。

所以拉马努金恒等式，更一般的形式是：


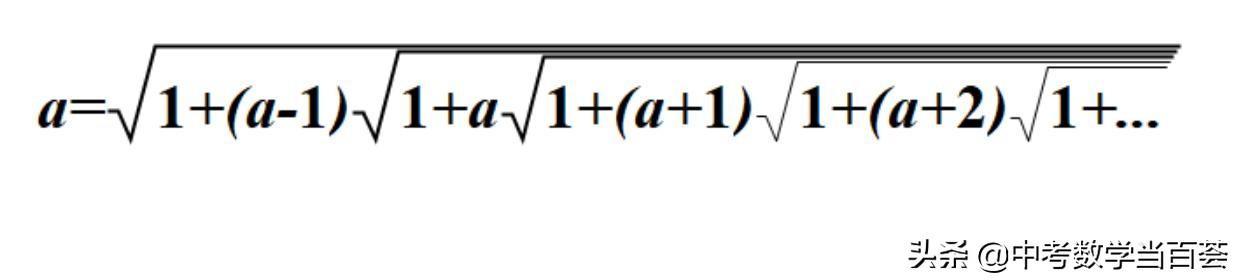
-04-结语

利用平方差公式和函数嵌套（复合函数）的思想，可以来说明他的正确性。虽然初中不提函数嵌套（复合函数）这种说法，但“整体思想”已经具备其雏形，所以上述证明过程，数学程度稍好的同学也可以看懂。

拉马努金没有受过正规的高等数学教育，但他靠自学沉湎于数论，尤其钟爱涉及π、质数等数学常数的求和公式和整数分拆。特别是他对数的直觉（数感）常常令人称奇，以至于亦师亦友的哈代感叹说：“我们学习数学，拉马努金则发现并创造了数学。”



标签：

相关推荐

​纪念“九一八”事件92周年

​纪念“九一八”事件92周年

217

纪念“九一八”事件92周年 我去过二次卢沟桥，第一次是2011年的5月，那时候和公司里的小伙伴们从北京CBD坐地铁转公交到了宛平县城，去实地考察一家对韩贸易公司。他们做的是出口...

​天秤座的15条特征，你中了几条？

​天秤座的15条特征，你中了几条？

155

天秤座的15条特征，你中了几条？ 脚本/ 醋醋 统筹/ 甜橙 制作/ 蚊子 制作/ 五毛君 催稿专员/ 靓仔青 十二星座每日运势 白羊座 爱情运有起伏，有问题不妨说出来，多能得到谅解的；事...

​＂当心吉普赛人!＂罗马地铁广播引巨大争议

​＂当心吉普赛人!＂罗马地铁广播引巨大争议

152

当心吉普赛人!罗马地铁广播引巨大争议 昨天（10日），罗马不少市民在乘坐A线地铁时，听到车厢广播添加了温馨提示——“当心吉普赛人”。 意大利Tgcom24网报道，在意大利有不少以“...

​“推迟”是delay，那“提前”的英文怎么说？

253

“推迟”是delay，那“提前”的英文怎么说？ 很多人知道“推迟”用英文怎么说，但不知道“提前”怎么说。 悄悄地问各位女生一个问题，你们平时最紧张的大姨妈「提前」或者「推迟...

​德鲁克经典著作简读

98

德鲁克经典著作简读 彼得·德鲁克（Peter F. Drucker，1909.11.19~2005.11.11），现代管理学之父，大师中的大师，其著作影响了数代追求创新以及最佳管理实践的学者和企业家们，各类商业管理...

​那些上过《男人装》的女明星,唐嫣马苏刘诗诗

​那些上过《男人装》的女明星,唐嫣马苏刘诗诗

91

那些上过《男人装》的女明星,唐嫣马苏刘诗诗 作者：孟大明白 本文来自微信号mengdaminbai 贫乳组 必须有周公子了，她拍了多次《男人装》，每次都不裸露。 和徐老怪凑一起完全是为了...

​《鬼吹灯》整本故事概览

​《鬼吹灯》整本故事概览

181

《鬼吹灯》整本故事概览 人点烛,鬼吹灯.相信这是所有灯迷们印象最深的一句话.今天,我们就概括下《鬼吹灯》系列共8部的主线故事. 鬼吹灯 清朝末年,一代奇人张三链子拥有三枚摸金符...